人間模様を数学する
数理モデリングによる建築・都市計画
建築学にとって「模型」は,自身のアイディアを伝えるための重要なツールです.デザインや構造など,伝えたい内容に応じて,その作り方や材料も変わってきます.このアナロジーに基づけば,空間の定量化を伝えるために,数式という材料を用いた,数学模型を作ることもできそうです.事実,この考え方は「数理モデリング」と呼ばれ幅広い分野で活用されています.
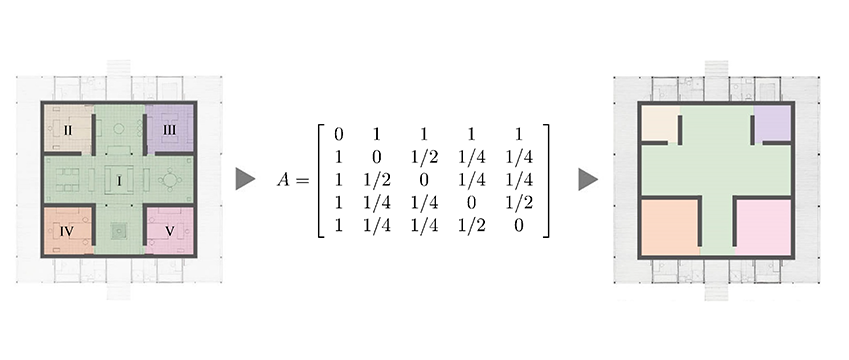
本間(裕)研究室では,建築・都市を定量化するための道具として数理モデリングを用い,その特性を把握し,より良い計画へと結びつけるべく,日々ディスカッションを重ねています.一例を挙げましょう.上図はフロアプランの最適化を試みた数理モデリングの例です.オフィスや商業施設といった建築物の設計では,フロアプランが非常に重要です.光・風といった環境や設備・構造要件の制約こそ満たす必要がありますが,できる限り,人の行き来がしやすい,あるいは賑わいのでるプランが理想的でしょう.言うなれば,人の流れを活性化する部屋の「場所」と「規模」を決める作業に他なりません.そのよう観点に基づけば,すでに存在している既存のフロアプランを(図-左),数式で表現することによって(図-中央),内部での行き来が最も活発となるよう再計算することなども可能になります(図-右).
人間模様を数学するために
建築・都市における「人々」や「行為」と,より密接に向き合うことが求められる計画分野では,数学的議論が十分に活用されてきたとは言い難い側面もあります.その理由としては,人々や行為を考慮するに当っては多様性が鍵であり,ひいては価値観の多様性を正面から扱う困難さに通じることが挙げられるのでは無いでしょうか.
かと言って,建築・都市計画に数学的議論は役立たないと結論付けるのも早計です.待ち行列理論に基づく施設規模論は,建築計画における定量的分析の有効性を示す最たる例と言えます.施設規模論が研究された当時より,理論・コンピュータの双方が格段の進歩を遂げているのですから.建築・都市計画でも数理モデリングが有効な局面は広がっているはずです.
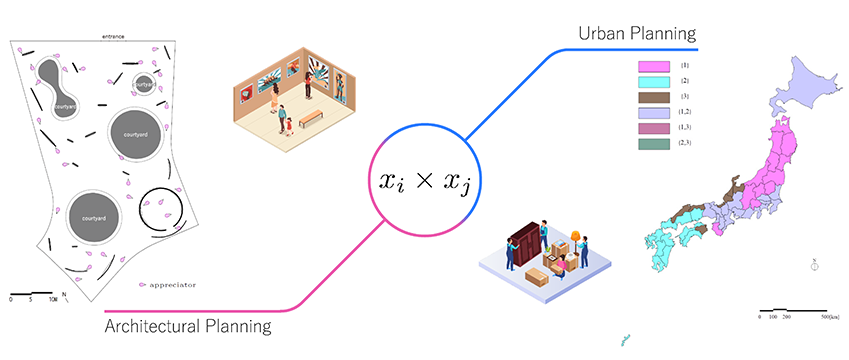
さまざまな人々によるさまざまな行為,すなわち「人間模様」の本質を表現する数理モデルの一つに,2次式≒掛け算が挙げられます.言わば,自身(xi)と他者(xj)との繋がりによる相乗効果(xi × xj)を考える訳です.2次式を用いることによって,例えば,美術館での鑑賞時に人が佇みやすい位置や(図-左),転勤による人口移動から導かれる地域のクラスター性(図-右)などを,より自然な形で追及できます.
建築・都市をシームレスに繋ぐ設計に向けて
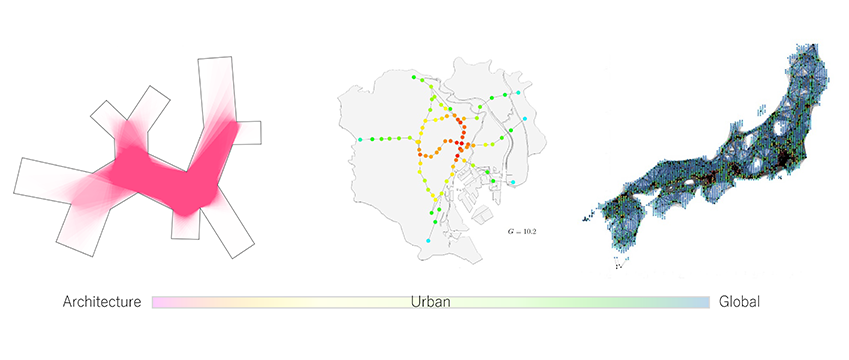
21世紀に目指すべき社会像として,持続可能社会・多世代共創社会が共通認識になりつつあります.複数の建築が集まり,町をつくり,都市をつくり,そして国をつくる,という事実を鑑みれば,建築あるいは都市といった言葉の縛りに囚われず,様々な分析スケールを跨いだシームレスな議論が,より一層重要となるのではないでしょうか.
ある単体の建築物が建つことによって都市にどのような影響が生じるのか.あるいは都市はその敷地にどのような建築物が建てられることを望んでいるのか.建築計画・都市計画に焦点を当てる研究室の一つとして,「建築⇔都市を繋ぐ」ことの本質を探究しています.
都市計画の目的が空間に対する方向性を示すことと仮定すると,建築計画の目的はその方向性ができる限り円滑に達成し得るよう空間の質を高めることとも解釈できます.空間には収容できる限界がある.空間の移動には距離負担が生じる.このような空間の構造的宿命を前提とした建築・都市のあり方を考えています.
